はじめに

今日では、様々な分析ツールの普及により、容易にデータの分析ができるようになりました。しかし、データ分析ではその手法によって解釈に大きな影響を及ぼすことがあるため、注意が必要です。今回は手法が解釈に影響を与えることを示す「シンプソンのパラドックス」を、マーケティングでのデータ分析を例に見ていきたいと思います。

シンプソンのパラドックスとは

シンプソンのパラドックス（Simpson’s paradox）は、データ全体とサブグループで分析結果が異なる現象のことを指します。1951年にイギリスの統計学者エドワード・H・シンプソンによって記述されたこのパラドックスは、統計学とデータ分析における基本的な問題を浮き彫りにし、データの解釈には慎重を期す必要があることを示しました。

全体とサブグループで分析結果が変わるという現象は、施策の効果検証などビジネスでのデータ分析の場面でもよく見られます。実務でデータ分析をしている方の中には、この現象が発生する仕組みを深く意識せずとも感覚的に理解し、うまく処理されている方も多いように感じます。以降では、このパラドックスがどのような仕組みで発生しているのか理解を深め、分析結果の解釈精度を上げていきたいと思います。

マーケティングのデータ分析例で考える

それでは、ここからシンプソンのパラドックスをマーケティングでのデータ分析に当てはめて具体的に見ていきましょう。

例として、あるECサービスで全顧客に向けてプロモーションコードを発行する施策を実施した場合を考えます。そして分析のテーマを「プロモーションコードの利用が購入金額にどのような影響を与えるか」と設定します。

データ全体での分析

まずは顧客全体でプロモーションコードの利用者と非利用者の平均購入金額を比較します。比較した結果、「プロモーションコード利用者は非利用者に比べて購入金額が低い」という結果が出ました。解釈としてはプロモーションコードは購買行動に悪影響を与えているということになります。

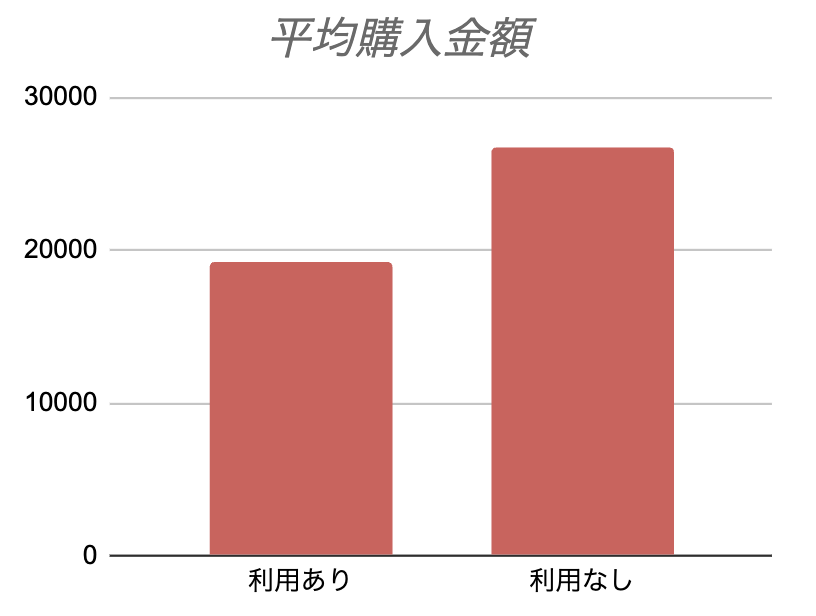
サブグループごとの分析

次に、顧客をサブグループに分けて分析します。ここではサブグループを「ロイヤル顧客（過去の購入金額が高い顧客）」と、それ以外の「非ロイヤル顧客」の2つに分類します。それぞれのサブグループごとにプロモーションコード利用者と非利用者の平均購入金額を比較したところ、両方のサブグループで「プロモーションコード利用者は非利用者に比べて購入金額が高い」という結果が出ました。解釈としてはプロモーションコードは購買行動に良い影響を与えているということになります。


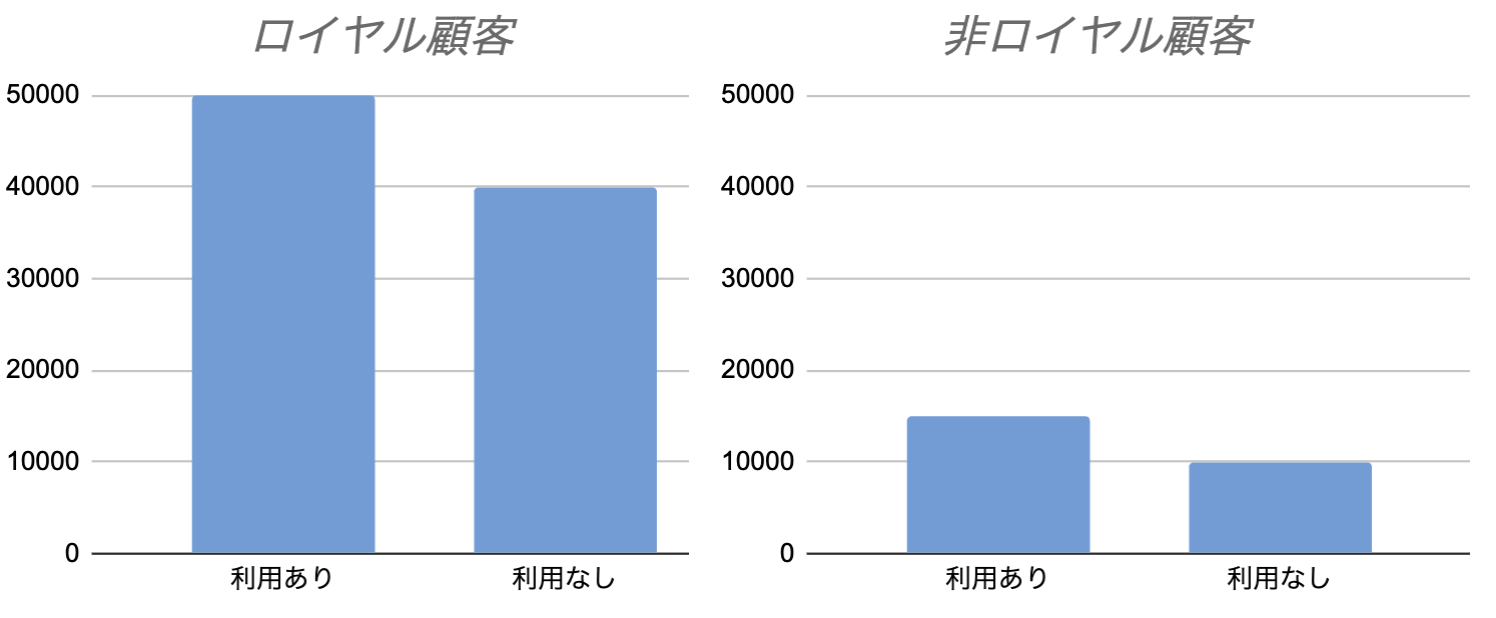
図2. サブグループによる購入金額の比較

パラドックスの解説

顧客全体とサブグループに分けた分析では真逆の結果となりました。これがシンプソンのパラドックスです。
なぜこのようなことが起こるのか解明するために、次の表1で顧客数の内訳を見てみましょう。

表1から以下の内容が読み取れます。

• プロモーションコードの利用者は非ロイヤル顧客の割合が高い
• プロモーションコードの非利用者はロイヤル顧客の割合が高い

これらは顧客全体での分析結果において以下のように言い換えることができます。

1. プロモーションコード利用者の平均購入金額は、非ロイヤル顧客の影響を強く受ける
2. プロモーションコード非利用者の平均購入金額は、ロイヤル顧客の影響を強く受ける

サブグループごとの分析結果（図2）をもう一度見てみましょう。

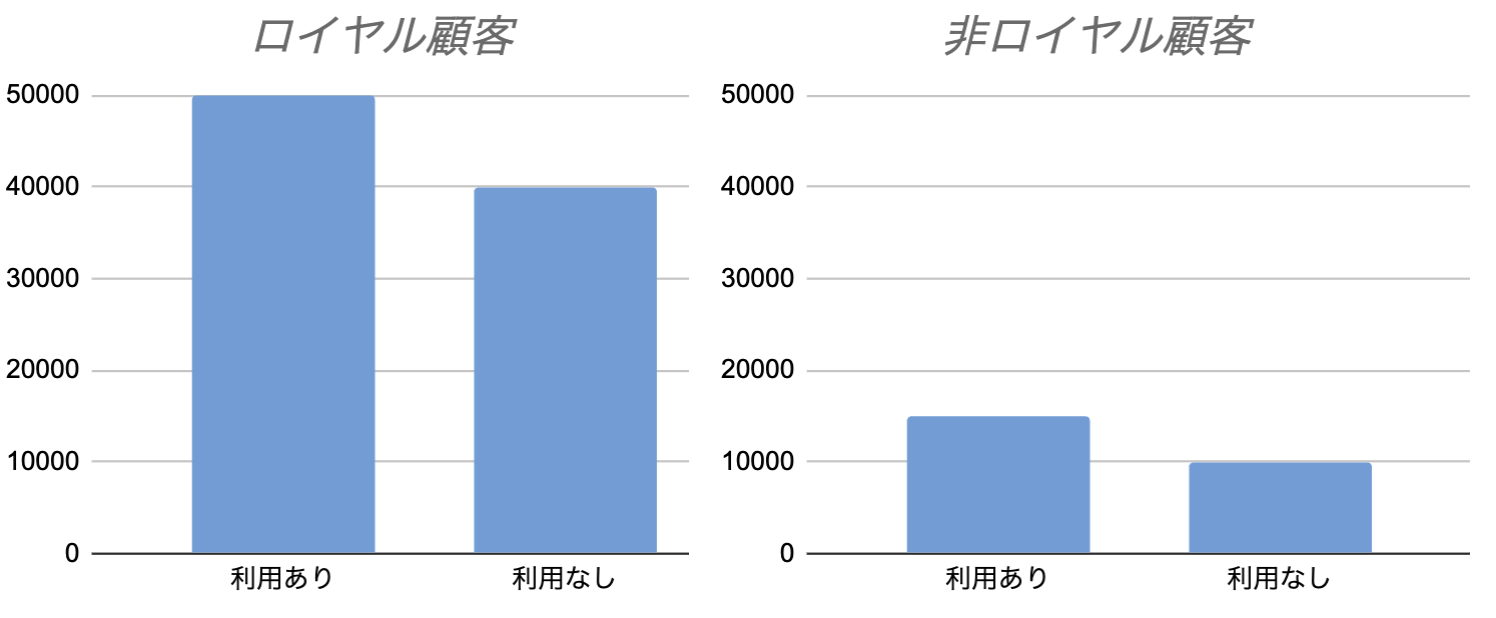
この図から、非ロイヤル顧客はロイヤル顧客と比べて、プロモーションコード利用有無に関わらず購入金額が低い傾向があることがわかります。これを踏まえて上記の1, 2を考えると、顧客全体での分析では「プロモーションコード利用者は非利用者に比べて購入金額が低い」という結果が出たことにも頷けるのではないでしょうか。ただし、この例ではサブグループの分析で得られた「プロモーションコードは購買行動に良い影響を与えている」という解釈の方が妥当だと考えられます。

誤謬を招く交絡因子

サブグループの分析では顧客全体を「ロイヤル顧客か非ロイヤル顧客か」（以下「ロイヤル分類」）に分類していますが、なぜその分類なのでしょうか。性別や年代など、データ次第で他の分類の選択肢もあるはずです。ここではロイヤル分類で分類することがどのような意味を持つのか見ていきましょう。

まず、今回の分析テーマに立ち帰ります。テーマは「プロモーションコードの利用が購入金額にどのような影響を与えるか」でした。つまりプロモーションコードの利用有無と購入金額の因果分析です。この因果における原因と結果は下記のように表現できます。

• 原因：プロモーションコードの利用有無
• 結果：購入金額

これまでの表1と図2で見てきたように、ロイヤル分類は以下の変数に影響を与えています。

• プロモーションコードの利用率
• 購入金額

つまり、ロイヤル分類は原因と結果の両方に影響を与えています。このように原因と結果の両方に影響を与える変数を交絡因子といいます。交絡因子が存在すると正しく因果を評価できません。今回の例では、非ロイヤル顧客であれば購入金額が低く、尚且つプロモーションコードを利用しやすいという傾向が、プロモーションコードの効果を過小評価させています。
プロモーションコードの効果を正しく評価するためには、交絡因子の影響を排除して分析する必要があります。サブグループの分析では、同じロイヤル分類（交絡因子）ごとに比較をすることで交絡因子の影響を排除しています。（なぜなら同じ属性同士のグループ内では属性による違いが存在せず、純粋に結果の比較ができるため）したがって、サブグループでの分析の方がより正しくプロモーションコードの効果を表していると考えられます。

このように同じ交絡因子を持つグループに分けることで交絡因子の影響を排除する処置を層別化といいます。補足として、交絡因子の影響の排除には重回帰分析も有効です。目的変数に「購入金額」、説明変数に「プロモーションコードの利用有無」と「ロイヤル分類」を設定すると、ロイヤル分類の影響（交絡因子の影響）も考慮した購入金額が得られます。この結果を利用してプロモーションコードの利用有無で購入金額を比較することで、交絡因子の影響を排除したプロモーションコードの効果が数値として得られます。

まとめ

分析結果の解釈の違いが重要な意思決定を左右することもあるため、手法の選定と結果の読み解きは慎重に行う必要があります。では分析者はどのように分析に取り組むべきでしょうか。

最も大事なのは分析者がデータのコンテクストを理解しておくことです。データを洞察し、それらのデータがどのような過程で生成され、またその生成過程でどのような影響を受け得るのか、ドメイン知識も駆使しながら考える必要があります。

今回はシンプソンのパラドックスを用いて手法が解釈に影響を及ぼす例を見てきました。ここでは交絡因子という言葉自体を知らなくても、データのコンテクストを理解していたら顧客全体での分析結果に違和感を抱くことができたかもしれません。その上で統計知識や手法の知識があれば、より適切な解釈や手法の選択ができると思います。本記事で交絡因子についての理解が深まり、分析結果の解釈精度を上げるヒントになれば幸いです。